相関次元解析 - カオス解析解説 -
カオスアトラクタの軌道は、一般にフラクタル構造を持つという特徴があります。フラクタル構造を有するか否かはフラクタル次元という特徴量を計ることにより判定できます。フラクタル次元が非整数であれば、フラクタル構造を有することを意味します。従って、フラクタル次元が整数になれば、変動はカオスでないことになります。フラクタル次元を計る方法として様々なものが提案されていますが、ここではカオス分析でよ く用いられるG-P法(相関次元法)について解析を行います。
G-P法(相関次元法)
GrassbergerとProcacciaにより考え出されたG-P法(相関次元法)は、アトラクタ上の任意の点における 半径rの超級と相関積分と呼ばれる量を計算することにより求めます。rとCrの対数を各埋め込み次元ごと に以下の図のようにプロットし相関図を求めます。
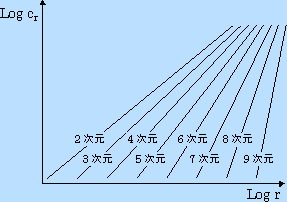
ここで、カオスや周期変動はある程度高い次元に埋め込むと、グラフの傾きは飽和するという性質があり、 その飽和したグラフの傾きを読み取ることにより相関次元(フラクタル次元)を求めることができます。

ここで、カオスや周期変動はある程度高い次元に埋め込むと、グラフの傾きは飽和するという性質があり、 その飽和したグラフの傾きを読み取ることにより相関次元(フラクタル次元)を求めることができます。
相関積分
●相関積分の定義
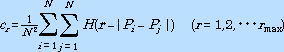
ここで、H(x)はx≧ 0 の時に1、x< 0の時に0を返すヘビサイド関数です。
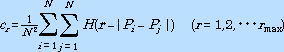
ここで、H(x)はx≧ 0 の時に1、x< 0の時に0を返すヘビサイド関数です。
●相関積分のアルゴリズム
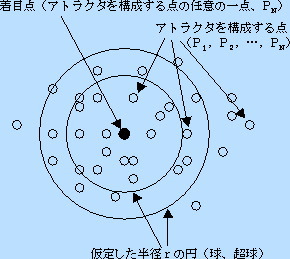
アトラクタを構成する点に含まれる任意の1点 P1と、 P 1を中心とする半径rの円(3次元では球、4次元以上では超球)を仮定し、 その中に含まれるアトラクタの構成点 P1の数を数えます。この操作をすべてのアトラクタ上のN個の点につ いて行うことで相関積分Crが求まります。

アトラクタを構成する点に含まれる任意の1点 P1と、 P 1を中心とする半径rの円(3次元では球、4次元以上では超球)を仮定し、 その中に含まれるアトラクタの構成点 P1の数を数えます。この操作をすべてのアトラクタ上のN個の点につ いて行うことで相関積分Crが求まります。




